√70以上 平均 の 公式 239582-平均の公式

標準偏差とは何か？ その求め方 Step①平均値を求める Step②偏差を求めて、2乗する Step③偏差の2乗の合計をデータの総数で割る Step④分散の正の平方根を求める 平均点が60点のテストで70点を取るのはどのくらいスゴイ事？ どうやってばらつきの大きさみんなの点数は平均点からだいたい24点ぐらいはなれてるってことね。 Step7 「偏差値の公式で計算」 標準偏差も計算できたら、 あとは 偏差値の公式にぶちこむだけ 。 偏差値の公式は、 偏差値 = 10×(自分の得点 – 平均点 )÷標準偏差 50 だったね？（解説） 平均値 e(x) という1種類の代表値だけでは，元のデータの散らばり具合が表せません． 次の図1の上の図と下の図とでは，平均値が同じですが，上の図ではデータが平均値付近に集まっているのに対して，下の図ではデータは散らばっており，これら2つのデータは異なる傾向を持ってい

Y Ax2乗の利用 平均の速さの求め方は変化の割合と同じだ 中学数学 理科の学習まとめサイト

平均の公式

平均の公式-平均値の変換公式とその証明 今、あるデータxとyがy＝axb という関係式で結ばれているとします。 この時、xの平均値をyで表すにはどのようにすればよいでしょうか？ 平均値の変換公式 \(\overline{y}=a\overline{x}b\)・・・（1）上の公式において，平均演算子「E」は，期待値 Expectation の頭文字からきているものです。上の式の中で，2つ目の公式が統計ではよく用いられます。覚えておいた方がよいでしょう。 一度に，理解できなくてもかまいません。

平均流速公式 等流 不等流 マニングの式 P408

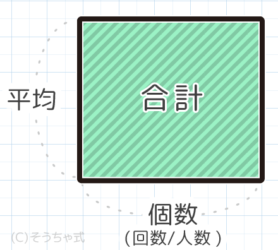
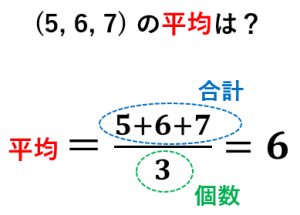
1台のレジがある。客の到着が1時間あたり平均12人であり，レジでの所要時間は平均3分であるとき，次の値を求めよ。 1 到着したとき，すぐにサービスが受けられる確率 2 系の中にいる人の平均人数 3 サービスを待っている人の平均人数5 二項分布の平均と分散二項分布B(n, p) の平均と分散は 平均：µ平均の求め方小学生公式 まずは、小学校で学習する平均に関する公式をまとめておきましょう。 ～平均の求め方～ 平均 合計 個数 ～合計の求め方～ 合計 平均 個数 平均の問題を解いていくためには、平均の求め方だけではなく、平均を利用して

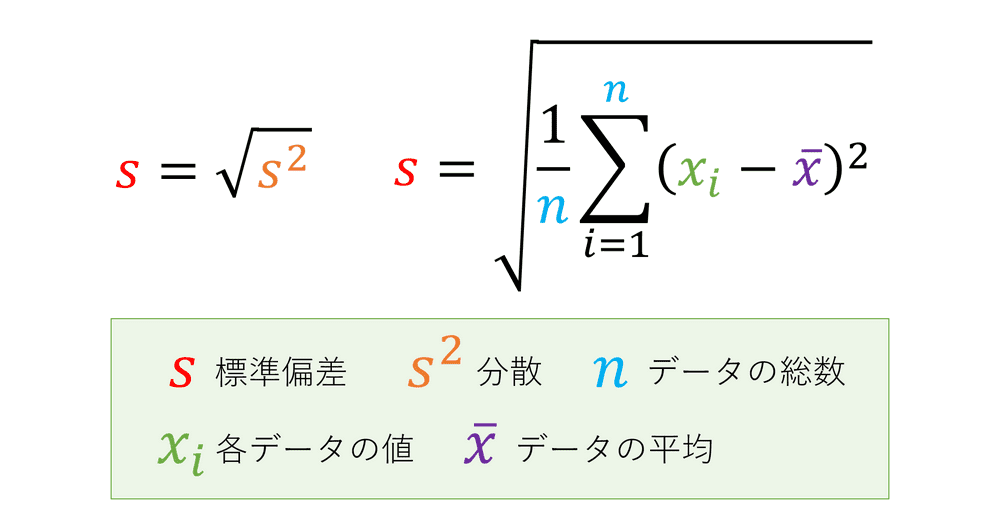
分散の公式① 分散を 、データの総数を 、それぞれのデータの値を , , , 、平均値を とすると、 （見切れる場合は横へスクロール） 偏差の 乗の和を求め、それをデータの総数で割れば、分散が求められますね。 公式② (2 乗の平均) − (平均の 2 乗) また、分散は (データの 乗の平均値) − (データの平均値の 乗) でも求められます。 分散の公式② 分散を 、データの値を 、データの平均標本平均 m の期待値 = μ 標本平均 m の標準偏差 σ'= 例 ある学校の3年生男子の平均体重が550(kg)で標準偏差が5(kg)のとき，その中から25人を無作為・復元抽出するとき，標本平均の期待値は550(kg)，標本平均の標準偏差は1(kg)となる．証明 離散的な場合 X = x i X = x i となる確率を P r ( X = x i) P r ( X = x i) と表すと、 X X の期待値 E ( X) E ( X) は、 と表される。 ここで、 n n は X X の事象の数である。 確率変数 X t X t は、 X X と値が t t だけ異なるので、 X t X t の期待値 E ( X t) E ( X t

と表す。 x − t グラフ ほかにも平均速度の例をいくつか考えてみよう。 たとえば、スタートしてから 5 秒後の位置は図の点 Iよって，分散は 「二乗の平均」 と 「平均の二乗」 の差なので 5180 − 4900 = 280 =280 5180 − 4900 = 280 となり，さっきと同じ答えになりました！ 分散の計算方法を2つ紹介しました： 方法1「平均からの差の二乗」の平均 方法2「二乗の平均」と「平均のそうすると、平均の速度 ¯v v ¯

小学５年生の算数 平均の求め方 練習問題プリント ちびむすドリル 小学生

算術平均 幾何平均 加重平均の計算 With Excel

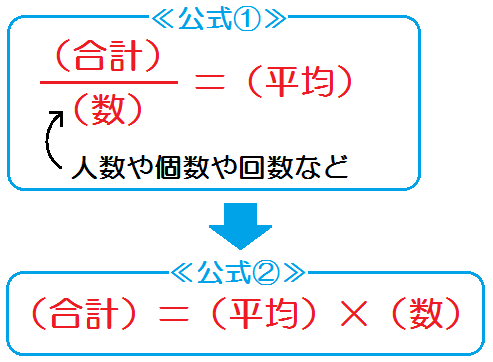
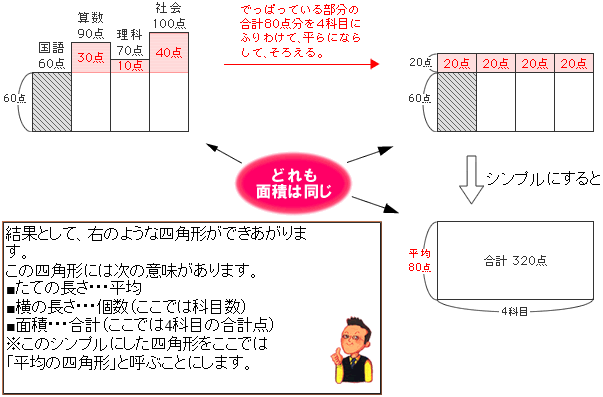
以前→「データの平均・分散・標準偏差の変数変換」において、 『データ』 の変量変換の式とその証明を紹介しました。今回は、 『確率変数』の場合の公式 を見ていきます。 期待値Eの公式 ・\(\mathrm{EaXb=aEXb}\) 上の式の証明を簡単に載せておきます。分散の公式 さて、ここからは数学として分散を扱っていきます。 さきほどの分散の求め方である、 平均値を出す;平均の公式 合計÷横に並べた数（人数など）＝平均 問題によっては、横に並べた数や合計が問われる場合もあります。 その時はこの公式を変形して 『平均×横に並べた数＝合計』 や 『合計÷平均＝横に並べた数』 などで計算しましょう。 平均のイメージができればわざわざ公式を覚える必要もありませんし、公式の丸暗記はかえって混乱を招くことがあるので、オススメしません。 ただ、平均算は

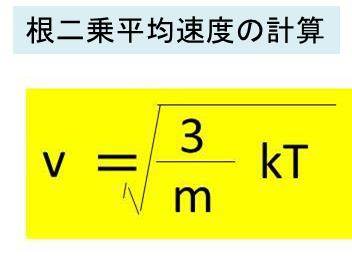
二乗平均速度と根二乗平均速度の公式と計算方法

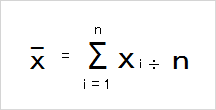
S シグマ を使った平均値の計算式

平均変化率は、公式の見た目が難しそうではありますが 実際にやってることは至ってシンプル \(x,y\)の変化量を求めて割ってるだけですね。 ただ、\(1h\)などの値を考える場合には 計算量が多くなっちゃうので、このように、 x − t グラフ上の2点を通る直線の傾きとして求まる速度のことを、その2点間の 平均速度 (average velocity) といい v ¯= E(X)=np 分散：σ2 = V(X)=npq = np(1−p) 6 確率変数の和の平均確率変数の平均について次の公式が成り立つ。 E(X Y)=E(X)E(Y) 7 互いに独立な確率変数の積の平均互いに独立な確率変数X, Y に対して

私 能力は平均値でって言ったよね 公式ガイドブック ネコ パブリッシング 版元ドットコム

分散とは 公式 求め方や計算問題 分散分析 多重比較の意味も 受験辞典

中学校の数学の「平均値の出し方」がわからん！ こんにちは、家で凍えそうなKenです。 中1数学の「資料と活用」で勉強する大切なことといえば、 平均値の出し方 です。平均値の出し方をしっていると日常生活でかな統計 標準偏差の意味と求め方 公式と計算例 標準偏差 とは、 データの散らばりの度合いを示す値 です。 標準偏差を求めるには、 分散 （それぞれの数値と平均値の差の二乗平均）の正の平方根を取ります 。 データが平均値の周りに集中していれば平均値は， \dfrac {} {7}=22 769 910 10 10 100 = 22 点 ほとんどの人が 10 10 点以下なのに一人の天才によって平均点が 10 10 点以上も上がってしまいました。 平均値のメリット：全てのデータを考慮できる。 平均値のデメリット：外れ値（異常に大きい値，小さい値）に弱い。 中央値の求め方と例 データを大きい順（または小さい順）に並べたと

統計学 第３回 西山 第２回のまとめ 確率分布 決まっている分布の 形 期待値とは平均計算 平均 合計 個数から卒業 平均 割合 値の合計 同じ平均値でも 同じ分散や標準偏差でも Ppt Download

標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ

＝ x2−x1 t2−t1 x 2 − x 1 t 2 − t 1 ＝ Δx Δt Δ x Δ t 図1 平均の速度 では、『 瞬間の速度 』はどのように求めるのでしょう？ 瞬間の速度 先ほど、『 瞬間のデータの個数をn、個々のデータを として、平均値を式で表すと以下のようになります。 (平均値) 平方和とは、個々のデータと平均値の差を二乗した値の和のことで、データが全体的にどの程度ばらついているかを表します。平均血圧と脈圧 平均血圧を知るのに役に立ちました。 脈圧については次の様に考えればよいと思います。 大動脈が水道管の如く固くなっているとすると、心臓の収縮時に血液が送り込まれるにも関わらず、大動脈がしなやかでないので膨らまず、血流量

平均の速さの求め方は 1分でわかる計算 公式 意味 はじきとの関係

しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは

よって、平均の速度を求める公式は次のようになります。 \begin{align} 平均の速度=\frac{\text{変位}\Delta{x}}{\text{かかった時間}\Delta{t}} \end{align} ちなみに山手線で東京駅を出発し、1周して東京駅に戻ってきたとき平均の速度は0です。と表します。 ¯v v ¯確率変数の和の分散の導出方法 次に，分散を求めていきます． こちらも先程の平均と同じように，周辺分布の分散をそれぞれ ， ，同時分布から求められる分散を ， とします． 確率変数の和の分散は，分散の公式を使用すると以下のようにして求められ

損失関数 評価関数 平均絶対誤差 Mae Mean Absolute Error L1損失 L1 Loss とは Ai 機械学習の用語辞典 It

小５算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ

男子の平均点と女子の平均点を合わせて $$(7581)\div2=78点$$ このようにはしちゃダメ！！ クラス全体の平均を出したいのであれば クラス全体の合計点を求めて、クラス全体の人数で割りましょう。 公式通りですね！ クラス全体の合計点とはデータの分析に関するさまざまな公式をまとめていきます。 詳細記事へのリンクも載せていますので、気になる問題や解き方があればぜひ参考にしてくださいね！ 目次データの代表値平均値 \\(\\bar{x}\\)中央値 \\(M_e平均の速さ＝道のりの合計÷時間の合計 平均の速さだからといって特別な公式はありません．速さの求め方と基本的には同じです． この問題の場合，「道のりの合計」は 12×2＝ 24km です． 「時間の合計」は往復それぞれにかかった時間を合計します

3

擬塑性流体の損失水頭 平均流速 P517

＝ 変位 時間 変 位 時 間 と、普通の速度の公式と同じように計算できますよ。 速度は v (速度を表す"velocity"の頭文字)と表しますが、平均の速度は v の上にバー (横棒)をつけて ¯v v ¯平均値を求める計算式は下記の通りです。 ()÷5 分子はデータの値の合計なので「点数の合計」、分母はデータの個数合計ですから「5」です。 よって平均値は ()÷5＝78点 です。 よって、元のデータは「各値が等しくなるよう均すと78点になる」ことが分かりました。 ＝ テストの平均値が高いほど「統計学では、平均値のことを指します。 平均値とは複数の数値に対して、個々を全て足し合わせた後、数値の個数で割った値のことを指します。 統計データを代表する値としてよく使われています。 文字式で表す際、文字の上にバーをつけて や などと表されます。 身近な例として、テストの平均点が挙げられます。 平均点は全ての人の得点を足しあわせ、人数で割ることによって

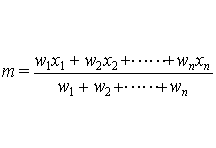
平均掲載順位と加重平均の話 リスティング広告 カルテットコミュニケーションズ

相加相乗平均まとめ 公式 証明 使い方 最小値 等号成立 理系ラボ

母平均の点推定を行うと、「不偏分散」のほかに「標準偏差」と「標準誤差」が出力されます。 標準偏差 標準偏差は母集団から得られた個々のデータのばらつきを表すものであり、分散の正の平方根で定義されます。 不偏分散が次の式から求められることは、18‐4章で既に学びました。

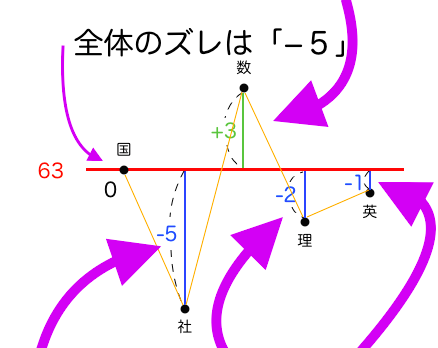
基準 仮平均 平均は賢く求めるよ 苦手な数学を簡単に

中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく

小５算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ

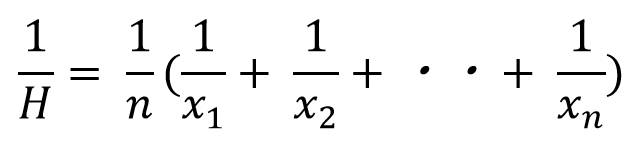
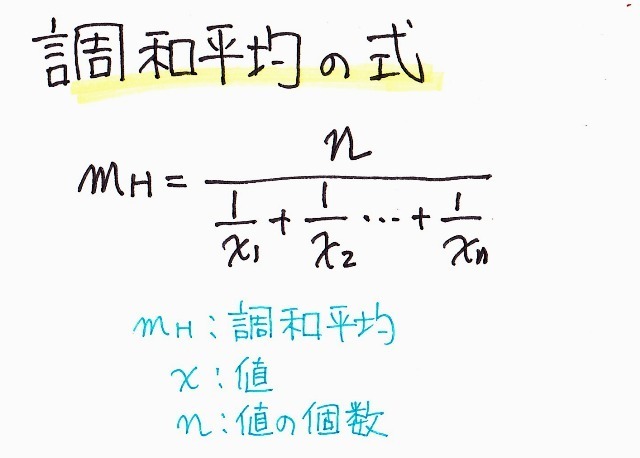
中学数学 理科 調和平均の考え方 速さから合成抵抗まで 偏差値40プログラマー

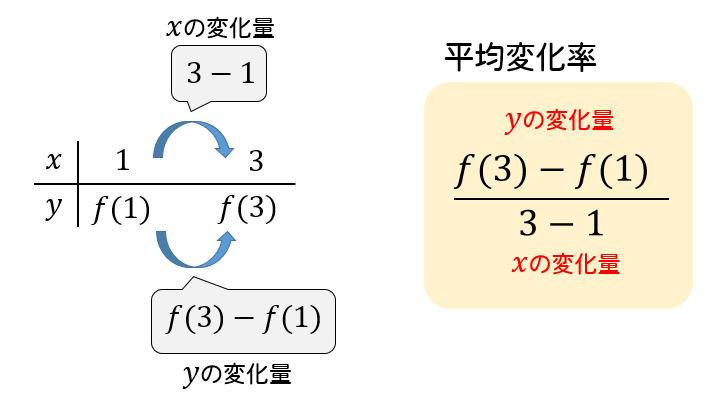
平均変化率とは 公式がややこしく見えるけど大丈夫 わかりやすく解いてみよう 数スタ

度数分布表からの平均値の求め方 中学数学 定期テスト対策 ベネッセ教育情報サイト

調和平均とは コトバンク

平均について

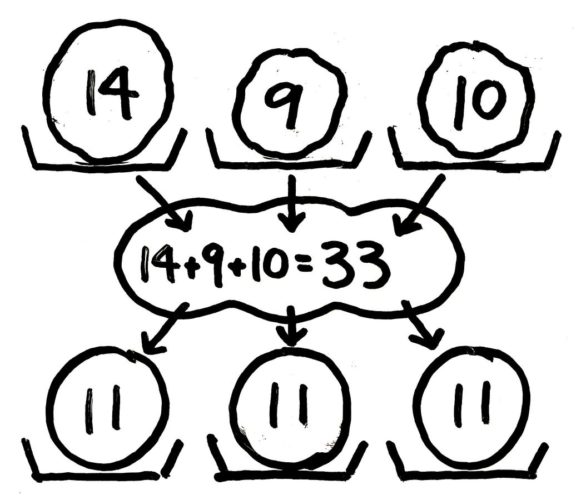
小学5 6年生 平均って何 求め方 問題の解き方をまとめました そうちゃ式 分かりやすい図解算数 別館

平均の求め方

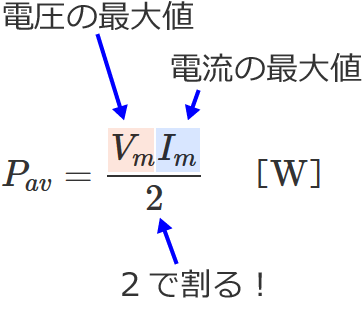
交流回路の電力の計算 抵抗だけの回路

平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ

3つの文字の時の相加 相乗平均の公式が成り立つ証明ですが一部スッキリしない部 Yahoo 知恵袋

度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

3 で相加相乗平均の式の所が分かりません Clearnote

Tvアニメ 私 能力は平均値でって言ったよね 公式サイト

平均 分散 標準偏差とは 後編 株式会社neoclassic

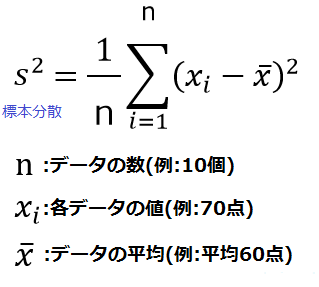
分散の求め方と公式 その有用性について アタリマエ

平均変化率と微分 微分係数との関係をわかりやすく解説 ネットdeカガク

第3回 暗号資産の損益計算 移動平均法 総平均法とは Line Bitmax 公式ブログ

算術平均 相加平均 と加重平均の違いは 重み ってナニ データ分析の解説 Haku1569 Excel でらくらく データ分析

５年算数平均 わかる教え方１

高校数学 平均値 と 平均値のとりうる値 映像授業のtry It トライイット

平均の速度と瞬間の速度の違いとは 公式および求め方

度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

Y Ax2乗の利用 平均の速さの求め方は変化の割合と同じだ 中学数学 理科の学習まとめサイト

平均 算数用語集

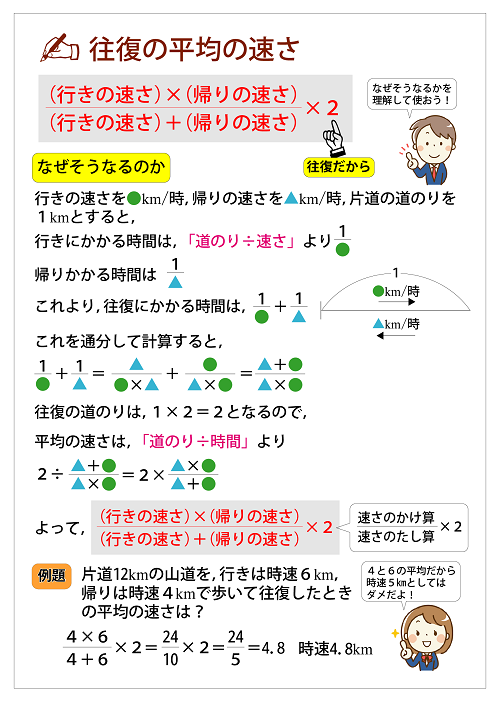
往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略

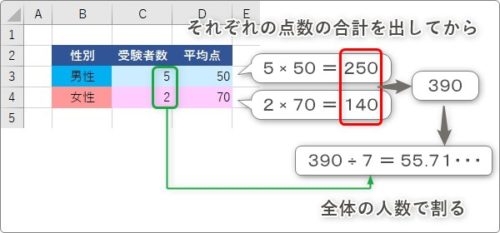
Excel エクセル での加重平均の計算式 加重平均の簡単な意味と説明 Prau プラウ Office学習所

微分と導関数の基本 平均変化率と微分係数から公式を理解する Irohabook

1

標準化 変量の変換 とは 仮平均についてもわかりやすく解説します 遊ぶ数学

1

中3 数学 平均の速さの求め方を解説 数スタ

仮平均を16として計算してみましたが答えと合いませんでした 計算ミスかもしれ Clearnote

数学 行き 時速80 帰り 時速 往復の平均時速は 温故知新ラーニング 楽天ブログ

流速とは 1分でわかる意味 単位 平均流速との関係 マニングの公式

高校数学 分散s と標準偏差s 分散の別公式 受験の月

５年算数平均 わかる教え方１

平均算を小学生に教えるための分かりやすい解説 問題の解き方 数学fun

データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典

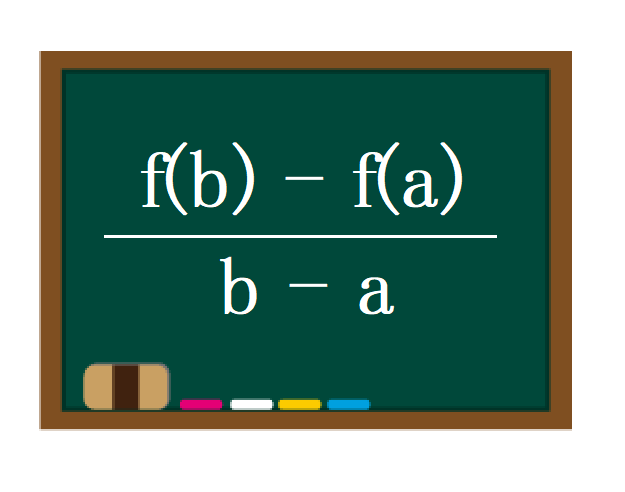
平均変化率の求め方 どんな関数でも公式一つで簡単に ヒデオの情報管理部屋all Rights Reserved

最も欲しかった 平均 の 公式 シモネタ

小学生算数 平均算のやり方を１からていねいにやってみよう 数スタ

流速とは 1分でわかる意味 単位 平均流速との関係 マニングの公式

中１数学 平均を文字式で表す問題を解説 数スタ

平均流速公式 等流 不等流 マニングの式 P408

ゆーノッポのモノ作りのアレコレ Ssブログ

三種類の 平均計算 を見てみよう 相加平均 相乗平均 調和平均

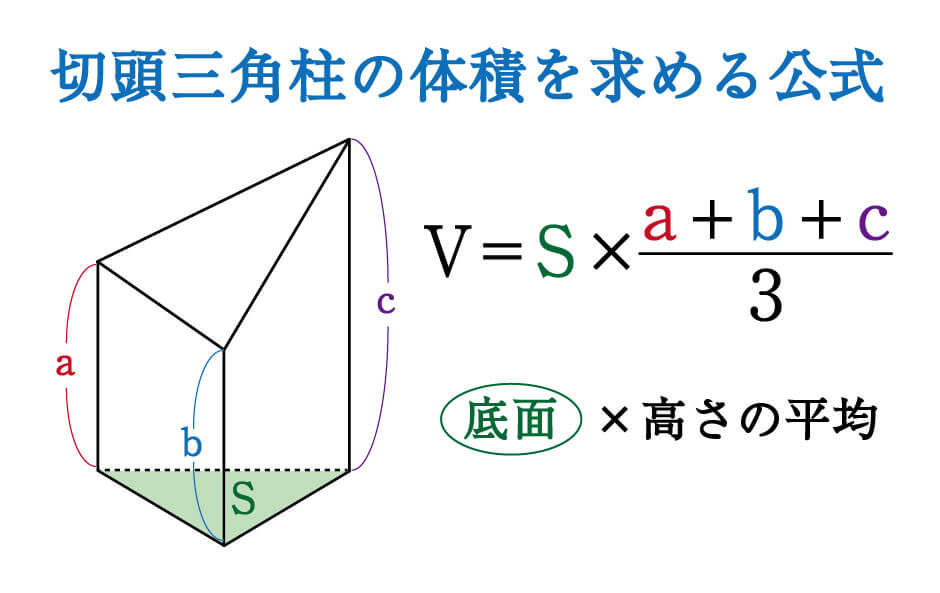
数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

統計学 第３回 西山 第２回のまとめ 確率分布 決まっている分布の 形 期待値とは平均計算 平均 合計 個数から卒業 平均 割合 値の合計 同じ平均値でも 同じ分散や標準偏差でも Ppt Download

データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典

放送大学 文字式 基礎数学 平均を確かめる 統計の基礎 ２ としきぴ堂 楽天ブログ

平均の求め方 小学生で学ぶ公式は 問題の解き方を解説 中学数学 理科の学習まとめサイト

標準偏差をエクセルの関数で求める方法とグラフの作り方 散布図 Office Hack

平均点が取れない 何をすればいいかわからない人向け 物理が苦手なのは公式を丸暗記しているから 物理 マナリンク

平均の加速度と等加速度直線運動の見分け方を教えてください どっちの公式を使え Clearnote

平均算を小学生に教えるための分かりやすい解説 問題の解き方 数学fun

平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語

に メンター保有状況による職務満足感の 平均値を示す 職務満足感の高さは 非公式メンター のみ有 14 6 3 5 Download Scientific Diagram

中学受験 平均算の解き方 面積図の書き方は 分かりやすく図解 そうちゃ式 受験算数 新1号館 数論 特殊算

中学数学 １次方程式 文章題の解き方 平均

平均値と中央値の違いとは 意味や特徴や数式などを簡単にわかりやすく いちばんやさしい 医療統計

使える 統計講座 深瀬勝範 第8回 統計的手法を使う 代表値と散らばり 人事のための課題解決サイト Jin Jour ジンジュール

調和平均とは データ分析の解説 Haku1569 Excel でらくらく データ分析

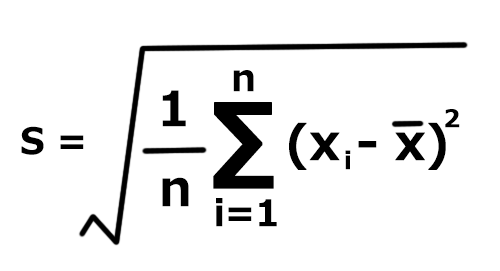
標準偏差をエクセルで求める方法と完璧なグラフの作 Udemy メディア

センター試験頻出 分散とは 求め方や意味を徹底解説 高校生向け受験応援メディア 受験のミカタ

相加相乗平均とは 公式 証明から使い方までが簡単に理解できます 練習問題付き 高校生向け受験応援メディア 受験のミカタ

平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ

Gogogo 待ち行列の計算はコレだけ覚えておくこと

Studydoctor平均値と仮平均での求め方 高校数学 Studydoctor

平均変化率 もう一度やり直しの算数 数学

中3数学 平均の速さの求め方 Y Ax2乗の文章問題を解説 Youtube

平均算 算数の教え上手 学びの場 Com

記録タイマーを使った物体の平均の速さの求め方 Hiromaru Note

1

分子速度の求め方や温度との関係性 分子速度の計算

度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

平均の求め方 計算式 と意味 欠点 具体例で学ぶ数学

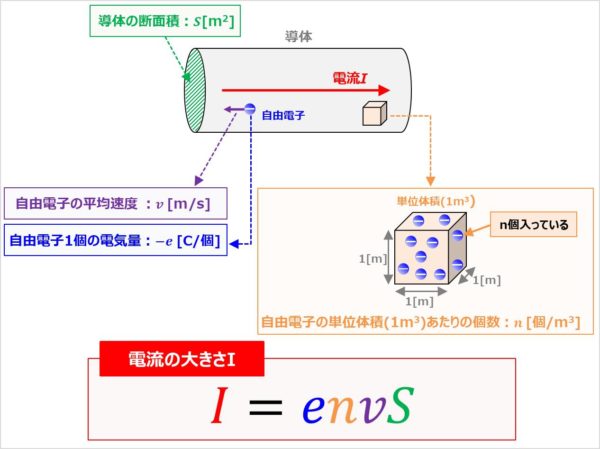
電流の大きさ I Envs の 導出 と 覚え方 について

統計学 第４回 西 山 Ppt Download

中1文字式 平均の表し方を解説 Youtube

分散の求め方についてです 1と2のときで求め方が違うのですがなぜですか Yahoo 知恵袋

小５ 算数 小５ ２１ 平均 Youtube

分散公式 ２乗の平均 ー 平均の２乗 Youtube

株がわかる 日経平均公式ガイドブック 第2版 日本経済新聞社インデックス事業室 本 通販 Amazon

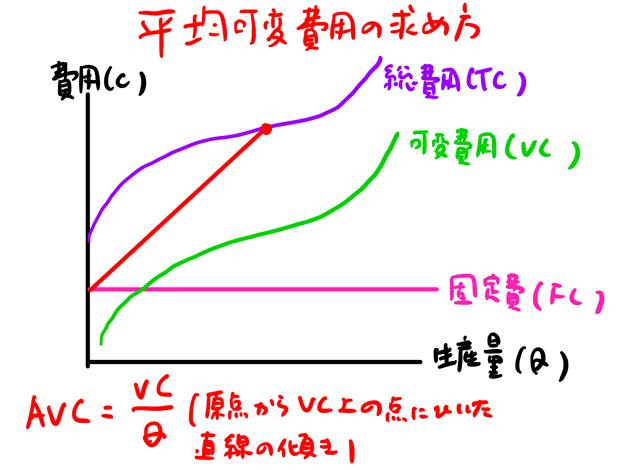
平均可変費用の求め方 中小企業診断士試験に出題される用語辞典

標本平均と標本分散とは 具体例と性質 証明付 理数アラカルト

Incoming Term: 平均の公式,